.fb-comments,.fb-comments span,.fb-comments span iframe[style]{min-width:100%!important;width:100%!important}

Seorang rekan mengalami kesulitan untuk menghitung peluang ekor yang cocok untuk suatu distribusi. Ingat bahwa tujuan distribusi kumulatif (CDF) digambarkan sebagai kemungkinan ekor kiri. Untuk variabel acak kontinu, X, dengan tujuan kerapatan f, CDF pada nilai x adalah


F(x)=Pr(X x)=f( t) dt

dimana integral dievaluasi pada interval (-∞, x). Artinya, itu adalah area di bawah tujuan kepadatan”di kiri diam”dari x.
Selain itu, peluang ekor yang benar adalah peningkatan jumlah ini. Peluang arah kanan ditentukan oleh


S(x)=Pr(X x)=1 – F(x)

Ini adalah lokasi di bawah kepadatan yang melakukan”sesuai”x.


Kemungkinan ekor yang sesuai juga disebut aspek kanan atau kemungkinan ekor atas. Performa, S, yang menyajikan probabilitas ekor ideal dinamakan survival distribution purpose (SDF).
Demikian pula, kuantil yang berhubungan dengan kemungkinan yang mendekati atau 1 bisa disebut kuantil serius.
Pos ini membahas mengapa perhitungan naif dari kuantil berlebihan bisa tidak akurat. Ini menunjukkan cara menghitung kemungkinan berlebihan dan kuantil parah dengan memanfaatkan fitur khas di SAS: 
Komputasi akurat dari kemungkinan intens

Rekan saya menghubungi saya untuk memeriksa beberapa masalah yang terkait dengan komputasi kuantil serius untuk p 1.
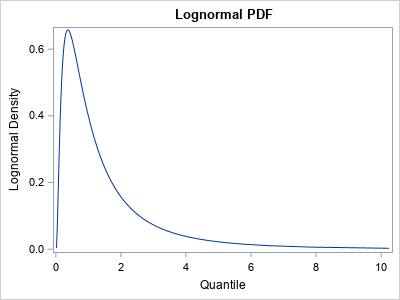
Untuk mendemonstrasikan, saya akan menggunakan distribusi lognormal umum, yang PDF-nya didemonstrasikan dengan tepat. (Di sisi lain, dialog ini berlaku sama dengan tepat untuk distribusi lain.)
Bila p sederhana, kuantil lognormal ditutup ke. 
Ketika p mendekati 1, kuantil lognormal besar secara sembarang karena distribusi lognormal tidak terbatas. 

Tahap Pengetahuan SAS berikut menggunakan operasi QUANTILE untuk menghitung kuantil luar biasa di sisa dan ekor ideal dari distribusi lognormal. Kuantil terhubung dengan peluang p=1E-k dan 
p=1 – 1E-k untuk k=8, 9, 10, …, 15.
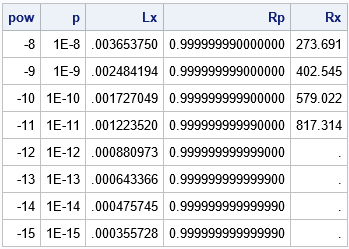

Kolom kedua menunjukkan probabilitas, p, dan kolom Lx menunjukkan kuantil ekor kiri yang sesuai.
Misalnya, baris pertama menunjukkan bahwa 1E-8 adalah probabilitas bahwa varian acak lognormal standar memiliki nilai kurang dari 0,00365.
Kolom Rp menunjukkan probabilitas 1 – p. Kolom Rx menunjukkan kuantil yang sesuai.
Misalnya, baris pertama menunjukkan bahwa 1 – 1E-8 adalah probabilitas bahwa varian acak lognormal standar memiliki nilai lebih besar dari 273.691.

Dari eksperimen, tampak bahwa fungsi QUANTILE mengembalikan nilai yang hilang 
ketika argumen probabilitas lebih besar dari atau sama dengan 1 – 1E-12.
Log SAS menampilkan catatan yang menyatakan


CATATAN: Argumen 2 berfungsi QUANTILE(‘Normal’,1) pada baris 5747 kolom 9 tidak valid.

Ini berarti bahwa fungsi tersebut tidak akan menghitung kuantil ekstrim-kanan. Mengapa?
Yah, saya dapat memikirkan dua alasan:

 Ketika p sangat kecil, kuantitas 1 – p tidak memiliki presisi penuh. (Ini disebut “masalah kehilangan presisi” dalam analisis numerik.) Faktanya, jika p lebih kecil dari epsilon mesin, ekspresi 1 – p PERSIS SAMA 1 dalam perhitungan floating-point! Jadi, kita membutuhkan cara yang lebih baik untuk menentukan probabilitas yang mendekati 1.

Untuk distribusi tak terbatas, fungsi CDF untuk distribusi tak terbatas sangat datar untuk nilai di ekor kanan. 
Karena kuantil pth diperoleh dengan menyelesaikan akar fungsi CDF(x) – p=0, perhitungan untuk menemukan kuantil kanan-ekstrim yang akurat secara numerik tidak tepat untuk distribusi tak terbatas.

Hitung kuantil ekstrem dalam SAS

Paragraf sebelumnya tidak berarti bahwa Anda tidak dapat menghitung kuantil ekstrem kanan. Ini berarti Anda harus menggunakan fungsi yang dirancang khusus untuk menangani probabilitas yang mendekati 1. Fungsi khusus adalah fungsi SQUANTILE, yang menggunakan ekspansi asimtotik dan trik lain untuk memastikan bahwa kuantil ekstrem kanan dihitung secara akurat. 
Jika x adalah nilai yang dikembalikan oleh fungsi SQUANTILE, maka 1 – CDF(x)=p. 
Tentu saja Anda dapat menulis ulang ekspresi ini untuk melihat bahwa x memenuhi persamaan
CDF(x)=1 – p. 

Sintaks untuk fungsi SQUANTILE hampir sama dengan fungsi QUANTILE. Untuk distribusi apapun, 
QUANTILE(“Distrib”, 1-p)=SQUANTILE(“Distrib”, p). Artinya, Anda menambahkan’S’ke nama fungsi dan mengganti 1 – p dengan p. Perhatikan bahwa dengan menentukan p bukannya 1 – p, probabilitas ekor kanan dapat ditentukan lebih akurat. 

Langkah SAS DATA berikut ini merupakan modifikasi dari langkah DATA sebelumnya. Ia menggunakan fungsi SQUANTILE untuk menghitung kuantil paling kanan: 
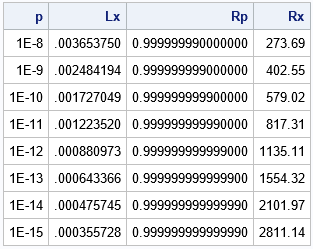

Tabel menunjukkan bahwa fungsi SQUANTILE dapat menghitung kuantil yang berada jauh di ekor kanan. 
Baris pertama tabel menunjukkan bahwa probabilitasnya adalah 1E-8 bahwa varian acak lognormal melebihi 273,69.
(Setara dengan, 1 – 1E-8 adalah probabilitas bahwa variannya lebih kecil dari 273.69.)
Baris terakhir dari tabel menunjukkan bahwa 1E-15 adalah probabilitas bahwa varian acak lognormal melebihi 2811.14.
Hitung probabilitas ekstrem di SAS

Ketika p kecil, 
“masalah kehilangan presisi”(mewakili 1 – p dalam presisi hingga) juga mempengaruhi perhitungan probabilitas kumulatif (CDF) dari sebuah distribusi. Artinya, ekspresi CDF(“Distrib”, 1-p)
mungkin tidak terlalu akurat karena 1 – p kehilangan presisi ketika p kecil.
Untuk mengatasi masalah itu, SAS menyediakan fungsi SDF, yang menghitung fungsi distribusi kelangsungan hidup (SDF).
SDF mengembalikan kuantil ekor kanan x dimana 
1 – CDF(x)=p. 
Ini sama dengan mencari kuantil kiri yang memenuhi CDF(x)=1 – p.

Langkah DATA berikut menghitung beberapa satu-probabilitas sisi. Untuk setiap nilai x, program menghitung probabilitas bahwa varian lognormal acak lebih besar dari x:
& #13
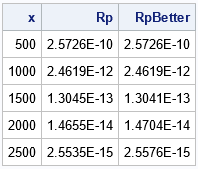
Perbedaan antara probabilitas di kolom Rp dan RpLebih baik tidak sedramatis kuantil di bagian sebelumnya. Itu karena kuantitas 1 – CDF(x) tidak kehilangan presisi ketika x besar karena CDF(x) 1. Namun, Anda dapat melihat perbedaan kecil antara kolom, dan kolom RpLebih baik akan cenderung lebih akurat ketika x besar.
Ringkasan

Artikel ini menunjukkan dua tip untuk bekerja dengan kuantil ekstrem dan probabilitas ekstrem. Ketika probabilitas mendekati 1, pertimbangkan untuk menggunakan fungsi SQUANTILE untuk menghitung kuantil. Ketika kuantil besar, pertimbangkan untuk menggunakan fungsi SDF untuk menghitung probabilitas.
Beri nilai pada postingan ini
Berbagi itu penting!
