.fb-comments,.fb-comments span,.fb-comments span iframe[style]{min-width:100%!important;width:100%!important}
& #13
Quando stavo creando Simulando i dati con SAS (Wicklin, 2013), esamino molti libri di testo introduttivi sulla simulazione Monte Carlo. Uno dei miei preferiti è 
Guida di Sheldon Ross Simulazione. (Sfoglio la 4a versione (2006) la 5a versione è stata pubblicata nel 2013.)
Mi piace che la riserva fornisca uno accanto all’altro molti esempi di scopi più brevi e di rapida comprensione dell’impiego di Monte Carlo approcci. Per diversi anni, ho bloggato su molti di questi programmi, come la stima di π o e applicando la simulazione in SAS. 

Questi esempi utilizzano variabili uniformi casuali per stimare una possibilità o una regione, quindi sono comprensibili da tutti coloro che hanno iniziato con la simulazione Monte Carlo. Questo breve articolo raccoglie questi esempi elementari in un’unica locale. Ogni sezione descrive brevemente il problema e fornisce un collegamento al sito Web a un articolo che mostra come risolvere il problema in SAS.
Stima π
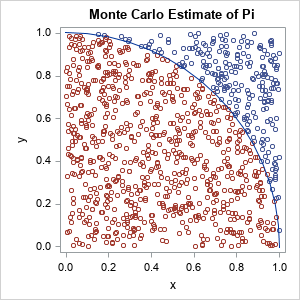

Ci sono molte tecniche per formulare il difficoltà di stima π ≈ 3,14159…. Il più popolare in particolare è identificato come il”processo del luogo”. Fornisci una grande quantità di fattori in modo uniforme e casuale nel quadrato dell’unità e conti quanti ce ne sono anche nel quarto di cerchio 
Q=x2 + y2 1, x ≥ 0, y ≥ 0. Il grafico per la destra illustra questo metodo. L’area del quarto di cerchio è stimata dal rapporto NC/NS, dove 
NC è il numero di punti all’interno del quarto di cerchio e 
NS è il numero di punti all’interno del quadrato unitario. Poiché sappiamo che il quarto di cerchio ha area π/4, una stima per π è 
π ≈ 4 NC/NS.
Ulteriori informazioni sulla stima di π come area.
Stimare l’area di una figura planare

Il metodo Monte Carlo può essere utilizzato per stimare l’area di qualsiasi figura planare limitata. Hai solo bisogno di un rettangolo di selezione e di un modo per valutare se un punto casuale si trova all’interno della figura. 
Ulteriori informazioni sulla stima delle aree utilizzando le tecniche Monte Carlo.
Il problema dell’ago di Buffon

Uno dei tanti metodi per la stima π fu introdotto da un nobile francese minore, G.-L. Leclerc, il conte de Buffon (il conte di Buffon). Secondo la leggenda, il conte lasciò cadere una pila di aghi su un pavimento di legno duro che aveva strisce di legno allineate in parallelo. Notò che alcuni aghi attraversavano le fessure tra le assi, mentre altri no. Ha quindi formulato uno dei primi problemi di probabilità geometrica: qual è la probabilità che un ago casuale attraversi una linea? La risposta generale dipende dalla larghezza relativa delle linee e dalla lunghezza degli aghi, ma se la lunghezza dell’ago è uguale alla larghezza tra le tavole, la probabilità è 2/π. Simulando questo esperimento, puoi stimare π.
Leggi di più sulla simulazione Monte Carlo dell’ago di Buffon.

Questo problema è anche collegato a un primo esempio di disonestà accademica. Nel 1901, Mario Lazzarini afferma di aver lanciato un ago 3.408 volte e di aver ottenuto una stima di π con un’accuratezza di sei cifre decimali. Quasi sicuramente ha mentito riguardo all’esperimento, ma la sua frode ci ricorda di rivedere criticamente affermazioni che sembrano troppo belle per essere vere. È facile usare una simulazione per mentire e ingannare. 
Stima e

Se un calcolo coinvolge un cerchio, non sorprende se nella risposta compare π. Tuttavia, è meno comune vedere la base del logaritmo naturale, e ≈ 2.71828…, apparire in un calcolo.
Tuttavia, e è la risposta a un problema molto semplice. 
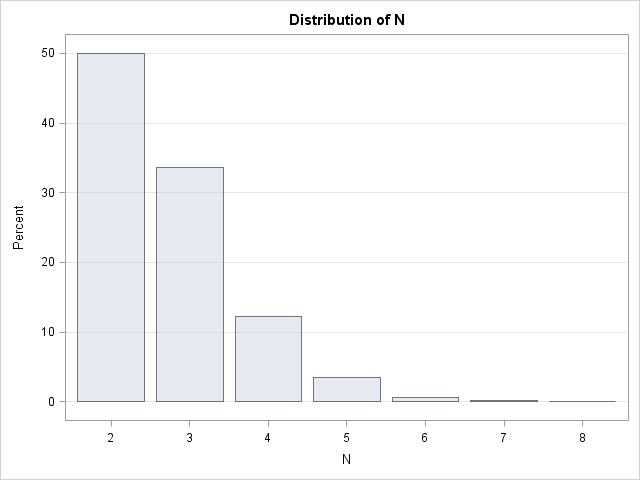
Sia N il numero minimo di estrazioni da una distribuzione uniforme tale che la somma delle variate ecceda 1. Qual è il valore atteso di N? Sappiamo che la risposta è maggiore di 1 e l’intuizione suggerisce che la risposta è maggiore di 2. Con un po’di matematica e geometria, puoi determinare che il numero previsto di variabili è e. 
Una simulazione Monte Carlo è facile da programmare utilizzando il passaggio SAS DATA in circa 10 righe di codice.
Ulteriori informazioni su come stimare e utilizzando una probabilità.
Stima di un integrale unidimensionale
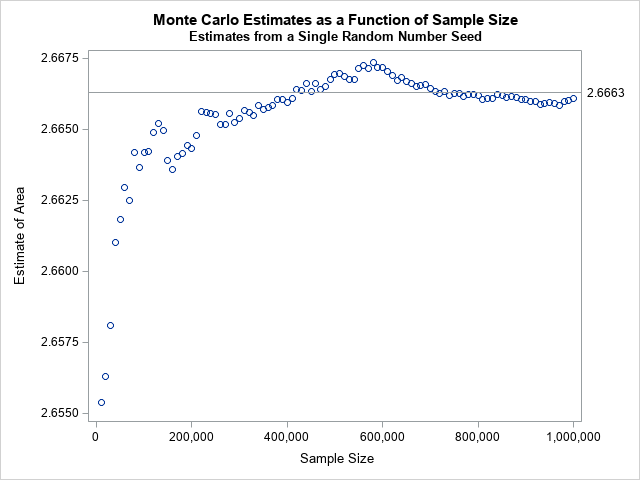

Usare il metodo Monte Carlo per stimare un integrale è un’esperienza illuminante. 
Per stimare l’integrale di una funzione continua g sull’intervallo (a,b), puoi generare un campione casuale uniforme in (a,b), valutare g su ogni punto del campione e prendere il media aritmetica di quei valori. In simboli, 

(int_a^b g(x) ,dx approx (b – a) cdot frac1n sumnolimits_i=1^n g(x_i))

dove le (x_i) sono variabili uniformi casuali indipendenti su (a,b).
Ulteriori informazioni sulle stime Monte Carlo di un integrale unidimensionale.
Stimare un integrale di dimensione superiore

Esistono molti metodi numerici per risolvere integrali unidimensionali. Esistono pochi metodi per risolvere integrali ad alta dimensione. Per un dominio rettangolare, il metodo Monte Carlo è sorprendentemente semplice da implementare. Per un dominio non rettangolare, il metodo è più complesso ma comunque più semplice di molti metodi concorrenti insegnati nei corsi di calcolo multivariato. 
Ulteriori informazioni sulle stime Monte Carlo di un integrale bidimensionale.
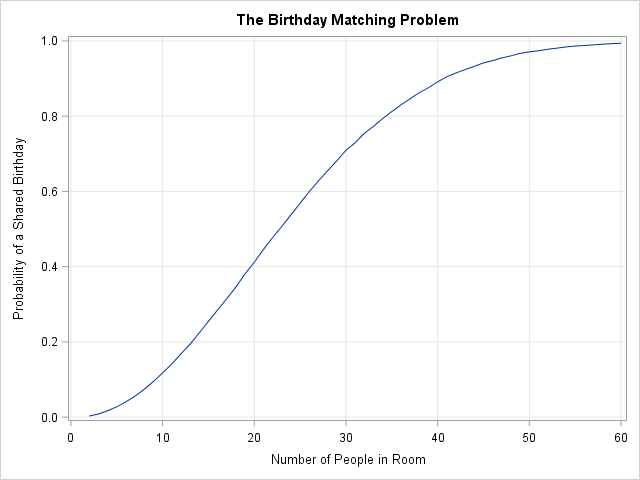
Il problema della corrispondenza del compleanno

Il famoso problema della corrispondenza del compleanno (a volte chiamato compleanno paradosso) afferma che in una stanza che contiene N persone, la probabilità che due persone condividano un compleanno è molto più alta di quanto suggerisce l’intuizione. In una stanza di N=23 persone, la probabilità che due persone condividano un compleanno è superiore al 56%. Per N=30, la probabilità è superiore al 70%.
Molte persone non credono al risultato finché non scrivono una simulazione che dimostri che è vero.
Ulteriori informazioni sulla corrispondenza del compleanno problema.
Il problema di Monty Hall

Monty Hall era un presentatore di giochi. Il problema di Monty Hall è una domanda sulla probabilità condizionata la cui risposta è contro-intuitiva. 
Supponiamo di essere in un programma televisivo e di avere la possibilità di scegliere tra tre porte: dietro una porta c’è un’auto dietro le altre, capre. Scegli una porta, ad esempio la n. 1, e l’ospite [Monty Hall], chissà cosa c’è dietro le porte, apre un’altra porta, ad esempio la n. 3, che ha una capra. Poi ti dice:”Vuoi prendere la porta n. 2?”È a tuo vantaggio cambiare la tua scelta? (Una capra era un modo divertente per dimostrare che il concorrente non ha vinto un premio.)

Molte persone sostengono che tu abbia scelto la porta che contiene il premio, oppure non l’hai fatto, quindi non ha senso cambiare. Tuttavia, si scopre che se si cambia, la probabilità di vincita è 2/3, mentre se non si cambia la probabilità di vincita è 1/3. Quindi, vale la pena cambiare idea!
Leggi di più sul problema Monty-Hall. 
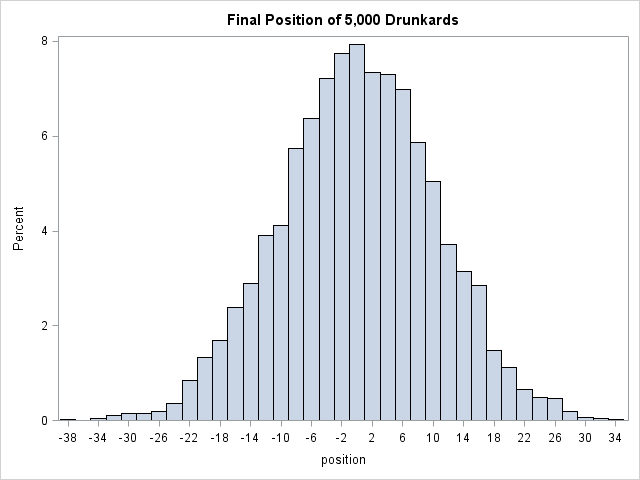
La passeggiata dell’ubriacone

La passeggiata dell’ubriacone è un tipo di passeggiata casuale. Il problema chiede la probabilità che un ubriacone (che fa un passo unitario in una direzione di coordinate casuali) torni alla sua posizione di partenza dopo N passi. Tuttavia, lo stesso calcolo può essere utilizzato per stimare la probabilità che finisca in qualsiasi altra posizione su una griglia unitaria. 
Puoi leggere come simulare la camminata di un ubriacone in una dimensione, o generalizzare il problema per simulare la camminata di un ubriacone in due dimensioni. 
Riepilogo

Questo articolo presenta diversi esempi classici che utilizzano la simulazione Monte Carlo per stimare un’area o una probabilità. Gli esempi sono facili da seguire perché simulano da distribuzioni uniformi e non richiedono alcuna conoscenza avanzata di probabilità o statistica. In quanto tali, questi problemi sono ideali per chi vuole iniziare a imparare come eseguire simulazioni Monte Carlo in SAS. Questo articolo raccoglie questi esempi in un’unica posizione comoda.
Valuta questo post
Condividere è importante!