Covariância e correlação são dois conceitos importantes usados em matemática para ciência de dados e aprendizado de máquina . Uma das perguntas da entrevista de ciência de dados mais frequentes é a diferença entre esses dois termos e como decidir quando usá-los. Aqui estão algumas definições e fórmulas matemáticas usadas que o ajudarão a entender totalmente a covariância versus correlação.
O que é uma matriz de covariância?
Uma matriz de covariância é usada para estudar a direção da relação linear entre as variáveis. Suponha que temos duas variáveis X e Y, então a covariância entre essas duas variáveis é representada como cov (X, Y). Se Σ (X) e Σ (Y) são os valores esperados das variáveis, a fórmula de covariância pode ser representada como:
Aqui estão alguns gráficos que destacam como seria a covariância entre duas variáveis em direções diferentes.
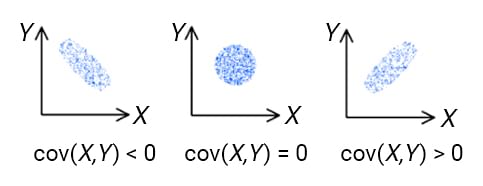
Fig: Valores de covariância e seus gráficos
Os valores de covariância da variável podem estar em qualquer lugar entre-∞ a + ∞. Um valor negativo indica uma relação negativa, enquanto um valor positivo indica uma relação positiva entre as variáveis. Quando o valor da covariância é zero, indica que não há relação entre as variáveis.
Quando a unidade de observação é alterada para uma ou ambas as variáveis, o valor da covariância muda. No entanto, não há mudança na força do relacionamento.
Para entender melhor a diferença entre covariância e correlação, vamos entender o que é uma matriz de correlação.
O que é uma matriz de correlação?
Uma matriz de correlação é usada para estudar a força de uma relação entre duas variáveis. Não só mostra a direção do relacionamento, mas também mostra o quão forte é o relacionamento. A fórmula de correlação pode ser representada como:
onde,
var (X)=desvio padrão de X
var (Y)=desvio padrão de Y
Quando as duas variáveis se movem na mesma direção, elas são positivamente correlacionadas. Ao contrário, quando as variáveis se movem na direção oposta, elas são negativamente correlacionadas.
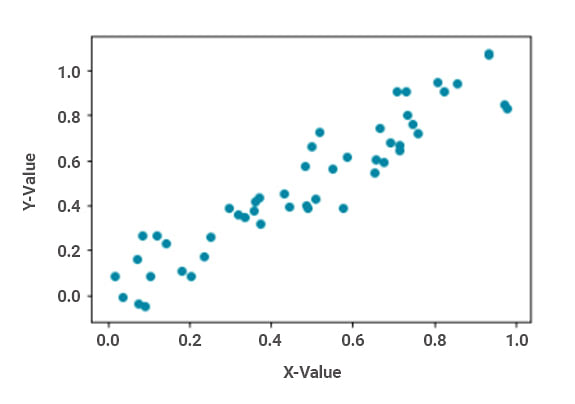
Fig: Relação positiva
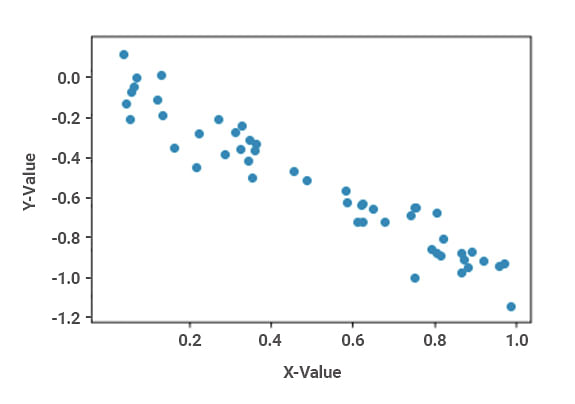
Fig: Relação negativa
O valor de correlação de duas variáveis varia de-1 a +1. Um valor próximo a +1 indica uma forte relação positiva e um valor próximo a-1 indica uma forte correlação negativa.
A correlação pode ocorrer de três formas:
-
Correlação Simples
A correlação é um único número que descreve o grau de relacionamento entre duas variáveis.
-
Correlação parcial
A correlação entre duas variáveis quando os efeitos de uma variável são removidos.
-
Correlação múltipla
Uma técnica estatística que prevê o valor de uma variável com base em duas ou mais variáveis.
A seguir, em nosso aprendizado das diferenças de covariância versus correlação, vamos aprender o método de cálculo da correlação.
Curso GRATUITO de ciência de dados com Python
Ganhe domínio em ciência de dados com Python agora Comece a aprender
Métodos de cálculo de correlação
Existem vários métodos para calcular o coeficiente de correlação. Aqui estão alguns dos mais comuns:
Coeficiente de correlação
Este é o método mais comum de determinar o coeficiente de correlação de duas variáveis. É obtido dividindo a covariância de duas variáveis com o produto de seus desvios padrão.
Coeficiente de correlação de classificação
Um coeficiente de correlação de classificação mede o grau de similaridade entre duas variáveis e pode ser usado para avaliar a significância da relação entre elas. Ele mede até que ponto, conforme uma variável aumenta, a outra diminui.
onde,
ρ=coeficiente de relação de classificação
D=diferença entre as classificações emparelhadas
N=número de itens classificados
Coeficiente de desvios simultâneos
O coeficiente de desvios simultâneos é usado quando você deseja estudar a correlação de uma maneira muito casual e não há muita necessidade de obter precisão.
onde,
rc=coeficiente de desvios concorrentes
n=número de pares de desvios
Continuaremos nosso aprendizado sobre as diferenças de covariância vs correlação com essas aplicações da matriz de correlação.
Aplicações da Matriz de Correlação
Existem três aplicações principais de uma matriz de correlação:
Para resumir grandes quantidades de dados
Quando há grandes quantidades de dados, o objetivo é ver padrões. Como tal, uma matriz de correlação é usada para encontrar um padrão nos dados e ver se as variáveis são altamente correlacionadas entre si.
Para inserir em outras análises
Outra aplicação comum de uma matriz de correlação para usá-la como entrada para outras análises, como análise fatorial exploratória, análise fatorial confirmatória, regressão linear e modelos de equação estrutural.
Para usar como diagnóstico para outras análises
A matriz de correlação também serve como diagnóstico para verificar outras análises. Por exemplo, em uma regressão linear, se houver um alto número de correlação entre os valores, isso sugere que as estimativas da regressão linear não serão confiáveis.
Veremos a seguir as aplicações da matriz de covariância em nosso aprendizado das diferenças de covariância vs correlação.
Aplicações da matriz de covariância
A matriz de covariância é muito útil como uma entrada para outras análises. Os mais comuns são:
Modelagem Estocástica
A decomposição de Cholesky é usada para simular sistemas com múltiplas variáveis correlacionadas. Visto que uma matriz de covariância é semi-definida positiva, ela é útil para encontrar a decomposição de Cholesky. A matriz de covariância é decomposta no produto de uma matriz triangular inferior e sua transposta.
Fig: decomposição de Cholesky ( fonte )
Análise do componente principal
Uma análise de componente principal é usada para reduzir a dimensionalidade de grandes conjuntos de dados. Uma decomposição automática é realizada na matriz de covariância para realizar a análise do componente principal.
Diferença: covariância vs correlação
Embora as matrizes de correlação e covariância sejam usadas para medir relacionamentos, há uma diferença significativa entre os dois conceitos. Aqui estão algumas diferenças entre covariância vs correlação:
|
Base para comparação |
Covariância |
Correlação |
|
Definição |
Medida de correlação |
Versão em escala de covariância |
|
Valores |
Situar-se entre-∞ a + ∞ |
Encontra-se entre-1 e +1 |
|
Mudança na escala |
Afeta a covariância |
Não afeta a correlação |
|
Medida sem unidade |
Não |
Sim |
Curso GRATUITO: Introdução à Análise de Dados
Aprenda conceitos, ferramentas e habilidades de análise de dados Comece a aprender
Semelhanças: covariância vs. correlação
A correlação e a covariância medem apenas as relações lineares entre duas variáveis. Isso significa que quando o coeficiente de correlação é zero, a covariância também é zero. As medidas de correlação e covariância também não são afetadas pela mudança na localização.
No entanto, quando se trata de fazer uma escolha entre covariância vs correlação para medir a relação entre as variáveis, a correlação é preferível à covariância porque não é afetada pela mudança na escala.
Aqui está o que você pode fazer a seguir
Um forte entendimento de conceitos matemáticos é fundamental para construir uma carreira de sucesso em ciência de dados. Isso garante que você possa ajudar uma organização a resolver problemas rapidamente, independentemente do setor em que você atua. Programa de Pós-Graduação em Ciência de Dados e o Programa de mestrado em ciência de dados em colaboração com a IBM ajudará você a acelerar sua carreira em ciência de dados e levá-la para o próximo nível. Este curso apresentará a aprendizagem combinada integrada de tecnologias-chave, incluindo ciência de dados com R , Python, Hadoop, Spark e muito mais. Também inclui projetos reais baseados na indústria em diferentes domínios para ajudá-lo a dominar os conceitos de Data Science e Big Data .
