Ik ga het hebben over de beveiliging achter Bitcoin-adressen en-sleutels, genaamd Public Key Cryptography. Dit omvat SHA256, Random Number Generators(RNG’s), Hash-functies en Elliptische kromme digitale handtekeningen (ECDSA.) Als je verder nog vragen hebt, stuur me dan gerust een DM. Ik ben een wiskundige van opleiding en ik heb er een diepe liefde voor. Als je merkt dat je een nieuwe interesse in cryptografie als hobby hebt, zijn er veel mensen die cryptografische algoritmen maken voor de lol, en hun gemeenschap kan nuttig zijn voor je reis.
Ik beloof dat je hiervoor alleen wat basisalgebra nodig hebt, evenals een eenvoudig begrip van exponentiële functies. Als u bekend bent met modulair rekenen, dat is geweldig. Zo niet, geen probleem.
Cryptografie bestaat al duizenden jaren en heeft momenteel een zeer robuuste gemeenschap van zowel professionals als hobbyisten. De technologie heeft een extreem lange weg afgelegd en de huidige iteraties zorgen voor de online beveiliging waar we nauwelijks over hoeven na te denken.
Laten we beginnen met het concept van Public Key Cryptography, specifiek binnen de context van Bitcoin. Op het meest basale niveau omvat PKC uw privésleutels en de openbare sleutels die daaruit worden gegenereerd. PKC maakt gebruik van de zogenaamde”valdeurfuncties” die gemakkelijk op te lossen zijn (gemakkelijk om een openbare sleutel van een privésleutel te genereren), maar bijna onmogelijk om te reverse-engineeren (een privésleutel vinden met een openbare sleutel.) Dit is vanwege het gebruik van modulaire rekenkundige, exponentiële functies en zeer grote priemgetallen.
Uw bitcoin-privésleutels zijn waarschijnlijk woorden, maar ze kunnen ook een heel groot aantal zijn. Om specifiek te zijn, wanneer we met de codering beginnen, worden uw privésleutels geconverteerd naar een groot aantal of binaire reeks (reeksen en nullen), ongeacht wat de oorspronkelijke vorm was. Hoe netjes! Dit is de reden waarom mensen soms zeggen dat uw privésleutels”een zeer, zeer groot aantal vertegenwoordigen”en de reden is voor de beveiliging ervan. Hoewel dit technisch waar is in deterministische/algoritmische zin, is het niet per se duidelijk waarom.
Het genereren van privésleutels is een ander interessant facet. Hardware-en bewaarportefeuilles doen dit voor u, en ze kunnen u al dan niet precies vertellen hoe ze dit doen (open-source versus closed-source software). Dit is zeker het overwegen waard bij het kiezen van een portemonnee. De andere optie is om je eigen helemaal opnieuw te maken. Je kunt een goede dobbelsteen gooien, een munt opgooien of een andere soortgelijke methode gebruiken. Er zijn ook online generatoren voor willekeurige getallen die zijn getest en beoordeeld door de professionele cryptografiegemeenschap. RNG’s gebruiken vaak de huidige tijd als hun generator om een klein aanvankelijk verschil te creëren dat, na voldoende iteraties, een totaal uniek getal oplevert. Kies een online RNG op eigen risico. Zelfs als de RNG zelf goed is, kan er malware op de site staan. Hoe meer je weet!
Dus we hebben onze geheime woorden. Laten we eens kijken wat er daarna gebeurt.
Dit is een heel eenvoudige vorm van onze luikfunctie.”G to the a mod n”vertegenwoordigt onze laatste openbare sleutel (mod is een afkorting voor modulaire rekenkunde, wat ons antwoord beperkt tot een bepaalde limiet van getallen, in tegenstelling tot elke afzonderlijke natuurlijk getal). Maar zelfs als u G en n kent, is er geen gemakkelijke manier om a te vinden, die uw persoonlijke sleutel vertegenwoordigt. Het berekenen van G naar de mod n is relatief eenvoudig, maar er is geen weg terug, dankzij de Discreet log-probleem. N is over het algemeen een groot priemgetal omdat ze per definitie niet kunnen worden ontbonden. Als relatieve complexiteit van functies/problemen u interesseren, kijk dan gerust eens naar Algoritme Tijdcomplexiteit.
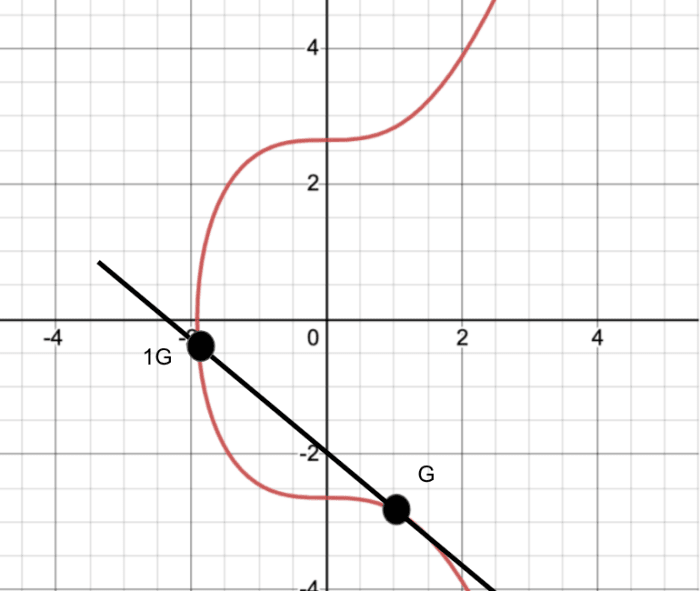
Laten we wat dieper ingaan en het grafisch bekijken voor een meer concreet begrip.
De rode lijn is onze curve, en is de specifieke die wordt gebruikt door Bitcoin’s ECDSA. G is het punt waar we beginnen, onze’generator’, zo u wilt. Dan gaan we G aan zichzelf”toevoegen”(hoewel het geen toevoeging is in de gebruikelijke zin-die gekke wiskundigen houden ervan om dingen opnieuw te definiëren. Laat me niet eens beginnen over topologie!). In dit geval betekent het toevoegen dat we de raaklijn van dit punt. Waar die raaklijn de curve ook snijdt, zal ons volgende punt zijn. We zullen opnieuw de raaklijn nemen en een nieuw punt vinden. In de praktijk (op een computer) gebeurt dit vele duizenden, of zelfs miljoenen keren. Het eindresultaat is dat zelfs als je weet waar ik ben begonnen, je niet weet hoe vaak ik G aan zichzelf heb”toegevoegd”om bij het laatste punt te komen. Hoe vaak we de toevoeging hebben uitgevoerd, is uw privésleutel (uw privénummer). Nogmaals, dit is gemakkelijk te controleren als een mogelijk antwoord wordt gegeven, maar bijna onmogelijk om’brute kracht’te gebruiken. Voila!
Dus we hebben onze eerste deterministische (één invoer geeft je één antwoord) door elkaar gooien van informatie, maar het is niet in een geweldig formaat (op dit moment is het gewoon een geordend paar (x,y). We hebben nu een openbare sleutel, afgeleid van een privésleutel. Laten we die informatie opnieuw versleutelen en transformeren.
We doen dit via SHA 256, wat staat voor Secure Hashing Algorithm Een hashing-algoritme is een specifieke reeks stappen die men op informatie toepast, wat resulteert in een versleutelde dataset van vaste lengte, ongeacht de lengte van de invoer.
Ja, deze familie van algoritmen is ontwikkeld door de United States National Security Agency (NSA), maar maak je geen zorgen. Het mooie van toegepaste wetenschap-inclusief wiskunde, is dat ontdekking en kennis onafhankelijk zijn van wie het heeft ontwikkeld. Daarom hebben we bewijzen. Als een bewijs’degelijk’is, staat het op eigen benen en kan het niet worden’gehackt’of omzeild. De SHA2-familie is algemeen bekend. Je kunt online gaan en de code bekijken, en als je wilt gebruik SHA256 zelf om sommige dingen te versleutelen. U zult merken dat een zeer kleine verandering in invoer een dramatische uitvoer op het antwoord zal hebben. Chaostheorie is prachtig. Maar hoe dan ook.
Omdat veel mensen miljarden dollars veiligstellen met SHA256, hebben ze ook veel geld uitgegeven om het te testen om de veiligheid ervan te garanderen. Mensen noemen kwantumcomputing vaak als een mogelijke manier om deze codering te doorbreken. Als kwantumcomputing echter mogelijk zou worden, kan er veel meer geld worden gestolen door de vijf grootste banken ter wereld te hacken. Ik weet zeker dat Bitcoin ver onderaan de lijst staat, want als het eenmaal is gehackt, zou de waarde ervan waarschijnlijk dramatisch dalen. Dat gezegd hebbende, als SHA256 in de toekomst minder veilig wordt, kunnen we de coderingsmethoden van Bitcoin altijd upgraden. Programmeerbaar geld!
SHA256 is vergelijkbaar met ECDSA in die zin dat het gemakkelijk is om een antwoord te controleren, maar erg moeilijk om brute kracht uit te oefenen-elk antwoord proberen totdat je het juiste vindt. SHA256 wordt zo genoemd omdat het een reeks van 256 bits creëert-een reeks van 256 nullen en enen. Dit zorgt voor een absurd hoog aantal mogelijke combinaties, meer dan het aantal atomen in het waarneembare heelal.
We gaan weer een andere hash gebruiken om een kleinere output te krijgen, waardoor voor een korter eindadres. Deze hashfunctie wordt RIPEMD-160 genoemd. Zodra we dit resultaat hebben, gaan we het omzetten in wat Base58 wordt genoemd, wat slechts een vorm is die beter leesbaar is voor mensen. Het laat zowel het cijfer nul (0) als de hoofdletter O (o) weg, zodat ze niet voor elkaar worden aangezien, evenals het weglaten van de hoofdletter I (i), zodat het niet wordt aangezien voor het cijfer één (1) of de kleine letter l (L) Het laat zowel het cijfer nul weg (0 ) en de hoofdletter O (o), zodat ze niet voor elkaar worden aangezien, evenals de hoofdletter I (i) weglaten, zodat deze niet wordt aangezien voor het cijfer één (1) of de lagere hoofdletter l (L).
En nu hebben we een openbaar adres dat aantoonbaar (in formele, wiskundige zin) is gemaakt op basis van een uniek privé-adres. Zelfs als alle zeven miljard mensen in de wereld duizend jaar lang elke dag een nieuwe openbare bitcoin-sleutel maken, zijn er zoveel mogelijkheden dat de kans om dezelfde twee keer te maken bijna nul is.
Dit is allemaal nogal een proces, het maken en verifiëren van sleutels, vandaar onze gemiddelde bloktijd van tien minuten. Tien minuten voor een wiskundig gegarandeerde eindafrekening is alles waard.
Dit is een gastpost van Nameless. De geuite meningen zijn geheel van henzelf en komen niet noodzakelijk overeen met die van BTC Inc. of Bitcoin Magazine.